4 SAS PROC MIXEDによる分析

階層的線形モデルは，何もHLM6を用いてしか分析できないというわけではない。 ¹ 基本的に階層的線形モデルは線形混合モデルと考えることができるので，線形混合モデルを扱えるソフトウェアであれば階層的線形モデルによる分析を行うことができる。

ここでは，SASにおいて混合モデルを扱うためのMIXEDプロシジャを用いて階層的線形モデルによる分析を行う方法について簡単に説明する。

SAS PROC MIXEDでは，HLM6とモデル式の表し方が若干異なる。

式(5)および式(6)を式(1)に代入して整理すると，

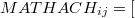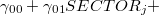$\displaystyle MATHACH_{ij} = [$	$\displaystyle \gamma _{00} + \gamma _{01} SECTOR_ j + \notag$	(7)
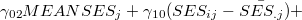$\displaystyle$	$\displaystyle \gamma _{02} MEANSES_ j + \gamma _{10} (SES_{ij} - \bar{SES_{.j}}) + \notag$	(8)
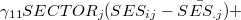$\displaystyle$	$\displaystyle \gamma _{11} SECTOR_ j (SES_{ij} - \bar{SES_{.j}}) + \notag$	(9)
$\displaystyle$	$\displaystyle \gamma _{12} MEANSES_{j} (SES_{ij} - \bar{SES_{.j}})] + \notag$	(10)
$\displaystyle$	$\displaystyle [ u_{0j} + u_{1j} (SES_{ij} - \bar{SES_{.j}}) + r_{ij} ] \label{eq.tougou}$	(11)

となる。このうち，最初の[ ]内は固定効果であり，2番目の[ ]内は変量効果である。 HLM6ではレベルごとに分けた式を入力できたのに対し，SAS（およびこの後で触れるR）においては，すべてのレベルを統合したモデル式(11)をもとに固定効果と変量効果の部分を分けて記述することになる。 SAS PROC MIXEDを用いた階層的モデルの分析方法について，詳しくは，Singer(1998)を参照されたい。

以下に，HSBデータを用いてHLM6を用いて行ったのと同じ分析をするためのプログラムの一例とその結果の出力を示した。

4.1 SASプログラム

***************************;
* SASによるHSBデータの分析 ;
*    By Taichi OKUMURA     ;
***************************;

OPTIONS ls = 80;

/* データの読み込み */
DATA hsb;
INFILE 'C:\Program Files\SAS Institute\SAS\V8\hsb-sas.dat';
INPUT id school ses mathach meanses cses sector;
RUN;

/* proc mixedによる分析 */
PROC MIXED DATA=hsb NOCLPRINT COVTEST;
CLASS school;
MODEL mathach = sector
                meanses 
                cses 
                sector*cses 
                meanses*cses / SOLUTION DDFM=bw NOTEST;
RANDOM intercept cses / TYPE = un SUB=school;
RUN;
QUIT;

以下に，MIXEDプロシジャの部分を簡単に説明しておく。

PROC MIXED

NOCLPRINT:: 集団（この場合はschool）ごとの結果は出力しない
COVTEST:: 分散要素の検定を行う

CLASS

schoolは数値ではなく，カテゴリ変数。

MODEL

この部分には固定効果の式を書く。

SOLUTION:: 固定効果の推定値を出力させる
DDFM=bw:: 固定効果の検定の際の自由度の設定
NOTEST:: 固定効果に関する仮説検定を行わない

RANDOM

この部分には変量効果の式を書く。

TYPE = un:: 分散・共分散行列に構造を仮定しない
sub=school:: 今回の例では，個々の生徒の観測値は学校（"school"）にネストされている

4.2 SASのアウトプット

上記のプログラムを実行したときのアウトプットを以下に示す。 ²

                                  SAS システム   


                              The Mixed Procedure

                               Model Information

             Data Set                     WORK.HSB
             Dependent Variable           mathach
             Covariance Structure         Unstructured
             Subject Effect               school
             Estimation Method            REML /* REML推定（デフォルト） */
             Residual Variance Method     Profile
             Fixed Effects SE Method      Model-Based
             Degrees of Freedom Method    Between-Within


                                  Dimensions

                      Covariance Parameters             4
                      Columns in X                      6
                      Columns in Z Per Subject          2
                      Subjects                        160
                      Max Obs Per Subject              67
                      Observations Used              7185
                      Observations Not Used             0
                      Total Observations             7185


                               Iteration History

          Iteration    Evaluations    -2 Res Log Like       Criterion

                  0              1     46724.22627510
                  1              2     46503.66454957      0.00000010
                  2              1     46503.66286827      0.00000000


                           Convergence criteria met.


                         Covariance Parameter Estimates

                                           Standard         Z
       Cov Parm     Subject    Estimate       Error     Value        Pr Z
/* レベル2の分散・共分散の推定値と有意性検定の結果 */
       UN(1,1)      school       2.3794      0.3714      6.41      <.0001
       UN(2,1)      school       0.1918      0.2043      0.94      0.3479
       UN(2,2)      school       0.1012      0.2138      0.47      0.3180
/* レベル1の分散の推定値と有意性検定の結果 */
       Residual                 36.7212      0.6261     58.65      <.0001


                                Fit Statistics

                     -2 Res Log Likelihood         46503.7 /* deviance */
                     AIC (smaller is better)       46511.7
                     AICC (smaller is better)      46511.7
                     BIC (smaller is better)       46524.0


                        Null Model Likelihood Ratio Test

                          DF    Chi-Square      Pr > ChiSq

                           3        220.56          <.0001

/* 固定効果（レベル2の偏回帰係数）の推定結果・有意性検定 */
                          Solution for Fixed Effects

                                  Standard
      Effect          Estimate       Error      DF    t Value    Pr > |t|

      Intercept        12.1279      0.1993     157      60.86      <.0001  /* G00 */
      sector            1.2266      0.3063     157       4.00      <.0001  /* G01 */
      meanses           5.3329      0.3692     157      14.45      <.0001  /* G02 */
      cses              2.9450      0.1556    7022      18.93      <.0001  /* G10 */
      sector*cses      -1.6427      0.2398    7022      -6.85      <.0001  /* G11 */
      meanses*cses      1.0392      0.2989    7022       3.48      0.0005  /* G12 */

Footnotes

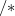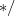ただし，検定の方法や反復計算の手法などが多少異なる場合がある。また，HLM6と異なり，この場合はデータセットを1つのファイルにまとめる必要がある。（具体的なデータは，*ページのRで用いたものと同様のものであるので参照されたい。）以下の例は，すでに整形したデータファイルを使用して分析したものである。
" $/*$ " 〜 " $*/$ "の部分はコメントである。